Briefly introduce the importance of electrical circuits in various applications.

Electrical circuits serve as the backbone of countless applications in our modern world. that have a wide range of industries like electronics, power distribution, telecommunications, and automation. These circuits/ networks enable the flow of electricity, allowing devices to function, information to be transmitted, and energy to be harnessed. need of electronics to solve daily problems and improve the quality of living standards.

nodal analysis is a fundamental technique for analyzing complex electrical circuits.

A key method for studying complex electrical circuits is nodal analysis. For electrical engineers and technicians, it is a vital tool since it offers a systematic and significant way to understand how currents and voltages disperse inside a circuit. Nodal analysis streamlines the process of resolving complex electrical issues by applying Kirchhoff’s Current Law (KCL) to circuit nodes, enabling effective circuit design, debugging, and optimization. Its capacity to handle complicated circuit topologies and support the creation of cutting-edge technology in a variety of sectors is what gives it its significance.

Understanding the Basics of Nodal Analysis

Define what nodal analysis is and its significance in circuit analysis.

1. Nodal analysis is a powerful method in electrical engineering used to analyze and solve complex electrical circuits. It relies on Kirchhoff’s Current Law (KCL), which states that the sum of currents entering a node in a circuit must equal the sum of currents leaving the node.
2. In nodal analysis, circuits are divided into nodes, where electrical currents meet, and branches, which are the paths connecting the nodes. By assigning voltages to the nodes and using KCL equations, you can determine the currents in various branches of the circuit.
3. The significance of nodal analysis in circuit analysis lies in its ability to simplify the process of solving complex circuits. It provides a systematic and efficient approach to understanding how currents flow and voltages distribute within a circuit.
4. Branch voltage and branch current are always remains fixed irrespective of reference.

Q. perform the nodal Equations.

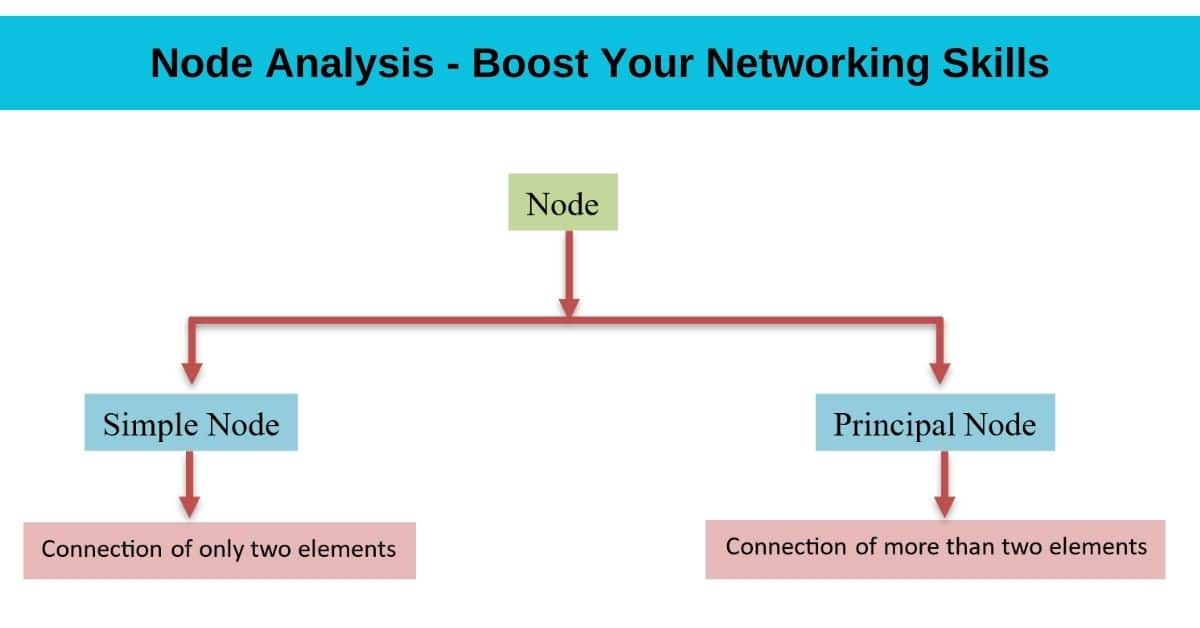
step 01: Identify the principal nodes in the circuits.

• Total principal node = 3 & Total simple node = 1
• Now be very carefully choose the reference
• choose reference -Principal node [ choose P₃ because the maximum branches is connected in circuit]
• Reference voltage: 0v is the most convent value
• can be any value of voltage (-∞ to +∞)

step 02: Assign the node voltage on each identified node.

• Vp1 and Vp2 are the node voltages.

Node 01- V_p1 (1/R₁ + 1/R₂) – V_p2 * 1/R₂ = I₁                                ………………. (1)

Node 02- V_p2 (1/R₂ + 1/R₃) – V_p1 * 1/R₂ = – I_{2 +} V₂/R₃              ………………. (2)

Note:

1. Node Voltage Depends on Reference
2. Branch Voltage Not Depends on Reference.

• Node voltage is always a variable quantity

The general KCL equation for a node is:

Iin−Iout=0

Where:

• Iin​ is the sum of currents entering the node.
• Iout​ is the sum of currents leaving the node.

Kirchhoff’s Current Law (KCL) and how it forms the foundation of nodal analysis.

Kirchhoff’s Current Law (KCL) is a fundamental principle in electrical engineering that forms the foundation of nodal analysis. KCL states that the algebraic sum of currents entering and leaving a node (a point in an electrical circuit where two or more branches meet) is always equal to zero. or we can say that, at any given node, the total current flow is equal to the total current flow out.

[ ΣI Node =0 ] / [ ΣI in = ΣI out ]

Note:

1. Node Voltage Depends on Reference
2. Branch Voltage Not Depends on Reference.

• Node voltage is always a variable quantity

The general KCL equation for a node is:

Iin−Iout=0

Where:

• Iin​ is the sum of currents entering the node.
• Iout​ is the sum of currents leaving the node.

Explain Kirchhoff’s Current Law (KCL) and how it forms the foundation of nodal analysis.

Kirchhoff’s Current Law (KCL) is a fundamental principle in electrical engineering that forms the foundation of nodal analysis. KCL st

ates that the algebraic sum of currents entering and leaving a node (a point in an electrical circuit where two or more branches meet) is always equal to zero. or we can say that, at any given node, the total current flow is equal to the total current flow out.

[ ΣI Node =0 ] / [ ΣI in = ΣI out ]

Here’s how KCL works and why it’s essential for nodal analysis:

1. Current Conservation:

KCL is based on the principle of current conservation, which means that electric charge is conserved in a closed circuit. In simpler words, the total amount of electric charge that enters a node [ ΣI in ] must equal the total amount of electric charge that exits[ ΣI out ] the node.  [ ΣI in = ΣI out ]

2. Node Analysis:

In nodal analysis, circuits are divided into nodes and branches. Nodes are points where currents converge or diverge, and branches are the paths connecting the nodes. Each node is assigned a voltage (with respect to a reference node that has 0 voltage), and KCL is applied to these nodes.

3. Mathematical Equations:

KCL is expressed as an algebraic equation for each node in the circuit. Mathematically, this is also written as ΣI_in = ΣI_out, where Σ represents the sum of currents.

4. Solving for Unknowns:

By applying KCL to multiple nodes in a circuit, you create a set of equations. These equations help you determine the currents at various branches and nodes. Solving these equations yields the values of interest, such as branch currents and node voltages.

5. Basis of Nodal Analysis:

Nodal analysis relies heavily on KCL. It’s a systematic approach where you apply KCL equations to all essential nodes in the circuit. These equations, along with Ohm’s law (V = IR), enable you to solve for the unknown voltages and currents in the circuit efficiently.

Formulating nodal equations in nodal analysis involves:

1. Identify essential nodes in the circuit.
2. Assigning voltages to these nodes.
3. Applying Kirchhoff’s Current Law (KCL) to each node and writing equations.
4. Expressing currents using Ohm’s Law (V = IR).
5. Combining KCL equations and current expressions to create a system of equations.
6. Solve these equations to find node voltages.
7. Using Ohm’s Law to calculate branch currents, providing a complete understanding of the circuit’s behavior.

Node analysis advantages and disadvantages:

Node analysis advantages	Node analysis disadvantages
1.     Systematic Approach	1.     Complex Node Identification
2.     General Applicability	2.     Increased Algebraic Complexity
3.     Reduced Equations	3.     Limited to Voltage Analysis
4.     Accurate Voltage Determination	4.     Limited for AC Analysis
5.     Clear Node Voltage Relationships	5.     Challenges with Nonlinear Components

Relation of nodal analysis with superposition theorem and Thevenin theorem:

• Superposition theorem helps simplify circuit analysis with multiple sources by considering each source individually.
• Thevenin’s theorem simplifies complex circuit sections into equivalent voltage sources and resistors.
• Nodal analysis is a method for solving circuits using Kirchhoff’s Current Law at nodes.
• Superposition and Thevenin can be combined with nodal analysis to simplify and analyse complex circuits effectively.

how to identify and label nodes and reference nodes.

1. write down the Label nodes with unique names (e.g., A, B, C… or 1, 2 ,3…) for analysis.
2. Make A reference node, often called the ground, is a chosen point for voltage measurements and simplifying the analysis.
3. Draw the circuit diagram, identify nodes at junctions, and designate a reference node.
4. Use voltage labels (e.g., Va, Vb, Vc… or V1, V2, V3…) relative to the reference node.
5. This setup aids in applying Kirchhoff’s laws and Ohm’s law for solving the circuit.
6. Understanding nodes and reference nodes is crucial for analyzing and solving electrical circuits.

Practical tips and strategies for simplifying nodal analysis for complex circuits.

In short:

1. Identify key nodes and choose a reference node (ground).
2. Use KCL equations and component relationships.
3. Simplify parallel resistors and apply source transformations.
4. Exploit symmetry or reciprocity if present.
5. Solve systematically and double-check your work.
6. Practice and build proficiency.
7. Consider circuit simulation software for extremely complex circuits.

With the help of this knowledge, we can build such kinds of projects like as PCB buildings, electronic prototypes, power electronics, audio and signal processing medical devices… etc

The Best comprehensive books for electronic which create solid foundations in circuit analysis

1. “Fundamentals of Electric Circuits” by Charles Alexander and Matthew Sadiku
2. “Electric Circuits and Networks” by K. S. Suresh Kumar

Frequently Asked Questions

1. When is nodal analysis used?

For analyzing the complex circuits where multiple nodes and sources are presents.

2. What is the node voltage of a branch?

The potential difference between two nodes of a circuits is known as a branch voltage.

Follow to the blog etechspark.com for more articles on electrical engineering and circuit analysis.

please leave your question in the comment section, give us your valuable feedback.